What is B-Tree
B-Tree is the B-tree we often say. We must not read it as a B-tree. Otherwise, it would be very shameful. B-tree data structures are often used to implement database indexing because of its high search efficiency.
Disk IO and read ahead
Disk read relies on mechanical motion, divided into three parts: seek time, rotation delay, and transfer time. The time-consuming addition of these three parts is a disk IO time, about 9ms. This cost is about 100,000 times that of accessing the memory; precisely because the disk IO is a very expensive operation, the computer operating system has optimized this: read ahead; every time IO, not only the data of the current disk address is loaded into Memory, but also the adjacent data is loaded into the memory buffer. Because the principle of partial pre-reading shows: When accessing an address data, data adjacent to it will be accessed soon. Each time the disk IO reads data, we call it a page. The size of a page is related to the operating system, usually 4k or 8k. This means that when a page of data is read, a disk IO actually occurs.
Comparison of B-Tree and Binary Search Tree
We know that the time complexity of the binary search tree query is O(logN), which is the fastest to find and the least number of comparisons. Since the performance is already excellent, why the index is implemented using the B-Tree rather than the binary search tree, the key factor Is the number of disk IOs.
The database index is stored on the disk. When the amount of data in the table is relatively large, the size of the index also increases, reaching several G or more. When we use the index to query, it is impossible to load all the indexes into the memory. Each disk page can only be loaded one by one. The disk page here corresponds to the node of the index tree.
A binary tree
Let's look at the times of disk IO in the binary tree search: define a binary tree with a tree height of 4 and find a value of 10:
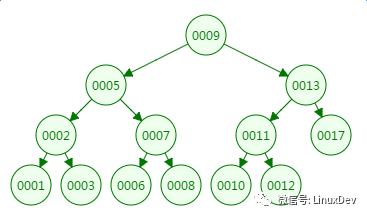
The first disk IO:
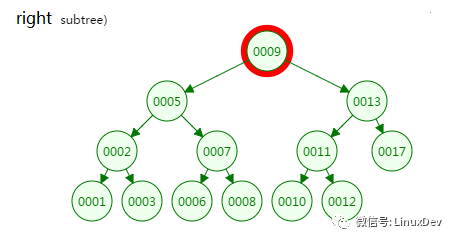
Second disk IO

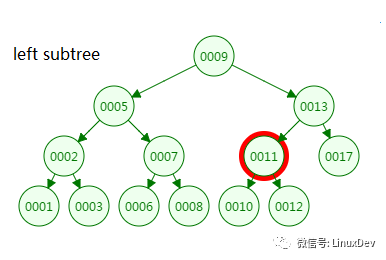
The third disk IO:
The fourth disk IO:
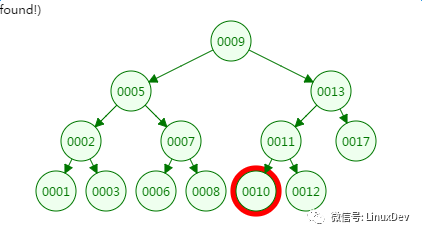
From the lookup process of the binary tree, the height of the tree and the number of disk IOs are all 4, so in the worst case the number of disk IOs is determined by the height of the tree.
From the previous analysis, the reduction in the number of disk IOs has to compress the height of the tree, so that the lean tree becomes a chunky tree as much as possible, so B-Tree was born in such a great era.
Second, B-Tree
The m-order B-Tree satisfies the following conditions:
1, each node has up to m subtrees
2, the root node has at least 2 subtrees
3. The branch node has at least m/2 subtrees (except the root node and the leaf node which are all branch nodes)
4, all leaf nodes are in the same layer, each node can have up to m-1 keys, and in ascending order
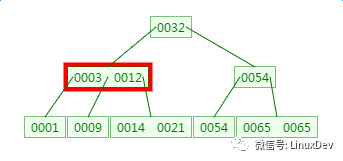
There is a 3rd-order B-tree as follows to observe the process of finding element 21:
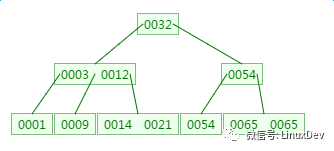
The first disk IO:
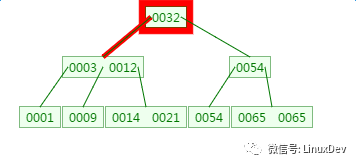
The second disk IO:
There is a memory match here: match 3 and 12 respectively
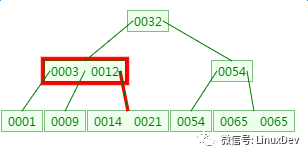
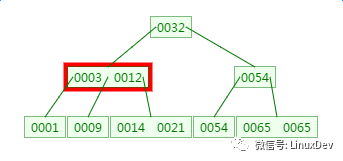
The third disk IO:
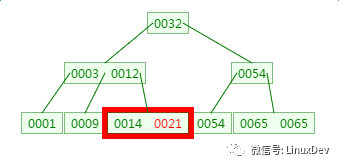
There is a memory comparison here, matching 14 and 21 respectively.
From the discovery process, the number of comparisons between the B-tree and the number of disk IOs is not much different from that of the binary tree, so this does not seem to have any advantage.
However, a closer look reveals that the comparison is done in memory and does not involve disk IO, which can be negligible. In addition, a node in the B tree can store many keys (the number is determined by the tree-level).
The same number of keys generated in the B-tree is much smaller than the nodes in the binary tree, and the number of nodes that differ is equivalent to the number of disk IOs. After reaching a certain amount, the difference in performance is revealed.
Third, the new B-tree
Add element 4 on the basis just above, it should be between 3 and 9:
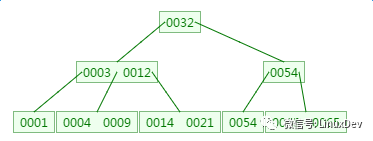
Fourth, delete the B-tree
Delete element 9:

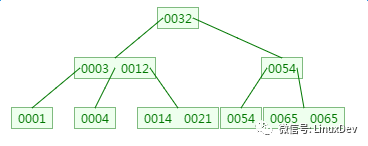
V. Summary
Inserting or deleting elements will cause fission in the nodes. Sometimes it will be very troublesome. But because of this, B-tree can always maintain multi-path balance. This is also an advantage of B-tree itself: self-balancing; B-tree is mainly applied to files The system and some database indexes, such as MongoDB, most of the relational database indexes are implemented using B+ trees.
The RIMA 6V AGM Battery is part of our UN series sealed lead acid battery,
UN series is a high quality VRLA battery, made of 99.997% pure lead, the battery is perfect designed for standby use, but also good at cycle use. The battery is based on AGM battery technology, which means that the electrolyte is absorbed by a fiberglass separator, preventing its leakage, this way the battery can work in any positions.
General Future:
5-12 years design life(25℃)
Non-spillable construction
Sealed and maintenance-free
High reliability and stability
High purity raw material: long life and low self-discharge
Standards:
Compliance with IEC, BS, JIS and EU standards.
UL, CE Certified
ISO45001,ISO 9001 and ISO 14001 certified production facilities
Application:
Uninterruptible Power Supply (UPS)
Emergency backup power supply
Auto control system
Communication power supply
Alarm and security system
Electric Power System (EPS)
6V Battery Rechargeable,6V Battery Power Wheels,6V Battery Ride On Toys,6V Battery 4.5 Ah
OREMA POWER CO., LTD. , https://www.oremabattery.com
